模板题

1、作用

查找区间最值（最大值和最小值）

时间复杂度为 O（nlogn）预处理

查询只需要 O（1）的复杂度

2、原理分析

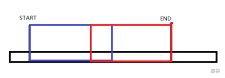
初始化就是复杂度最高的，也是较难理解的
可以将 i~j 的一块区域分为左边和右边来求解

因为是求最值 不是和或差 所以是成立的
如图

3、数组的定义

1
2
3
f[i][j] 
//代表从第i个数开始(包括自身)
//向后延伸 2的j次方 个数的最值

所以

1
f[i][0] //就是第i个数的值

4、处理

我们可以枚举j，i来求出最值

当然不要忘了赋初值
循环j，i（不要越界）

1
2
3
4
5
6
int i, j;
for(j = 1; j <= log2(n); j++) {
	for(i = 1; i + (1 << j) - 1 <= n; i ++) {
		f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
	}
}

5、代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<bits/stdc++.h>
using namespace std;

const int maxn = 1e5 + 2;
int n, v[maxn], m;
int f[maxn][35];

int read();
#define r1 read()

void ST_prepare() {
	int i, j;
	for(j = 1; j <= log2(n); j++) {
		for(i = 1; i + (1 << j) - 1 <= n; i ++) {
			f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
		}
	}
} //查找区间最值 

int ST_ask(int st, int ed) {
	int mid = log2(ed - st + 1);
	return max(f[st][mid] , f[ed - (1 << mid) + 1][mid]);
}
int main() {
	int i, j, x, y;
	
	n = r1;m = r1;
	for(i = 1; i <= n; i ++) {
		v[i] = r1;
		f[i][0] = v[i];
	}
	
	ST_prepare();
	
	for(i = 1; i <= m; i ++) {
		x = r1;
		y = r1;
		printf("%d\n",ST_ask(x,y));
	}
	
	return 0;
}

int read() {
	char c = getchar();
	int x = 0,f = 1;
	for(; !isdigit(c); c = getchar()) if(c == '-') f = -1;
	for(; isdigit(c); c = getchar()) x = (x << 1) + (x << 3) + (c ^ 48);
	return f * x;
}

有错请大佬纠正